The New Noise-Reduction Technology

enhances existing FM stereo reception technology:

  • up to 22 dB less noise while preserving stereo separation
  • reduction of all types of interference including multipath interference and interference from IBOC signals
  • only L and R needed as input signals
  • undisturbed audio signals are passed audibly unchanged
  • can be connected as a stand-alone device to existing receivers or audio post-processing units
  • software-based solution (C-Code available), portable to software-designed radio (SDR)
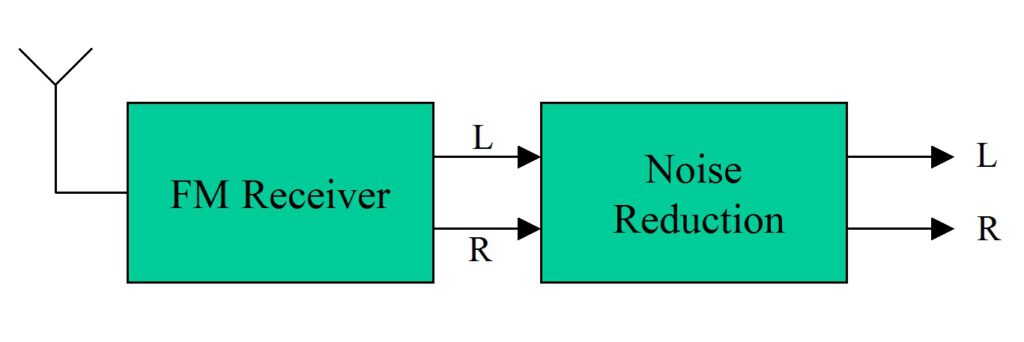
Figure 1 | Noise reduction of the L and R signals of an FM stereo receiver

The main idea behind it

With FM stereo the left and right audio signals are transmitted in matrixed form, i.e. as a sum signal (L+R)/2 and a difference signal (L-R)/2 * . This is done in the stereo encoder at the FM transmitter site. In the FM stereo receiver the FM signal is demodulated. The sum and difference signals are dematrixed to get the left and right audio signals back again.

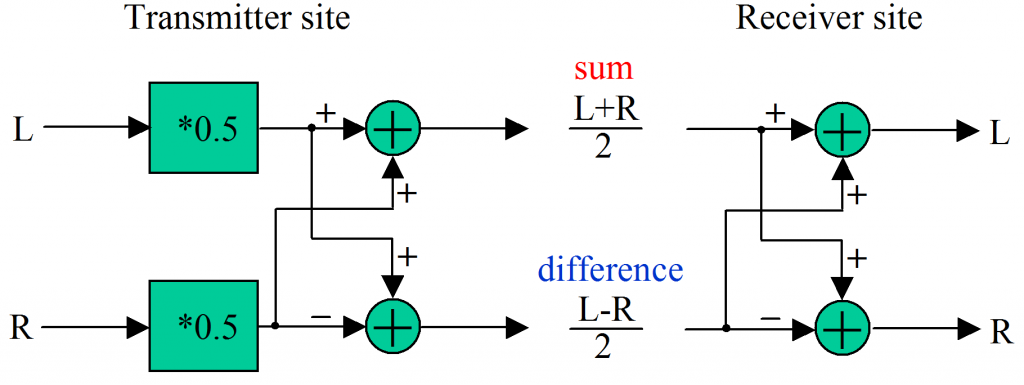
Stereo transmission in matrixed form
Figure 2 | Stereo transmission in matrixed form

The matrixing and dematrixing rules are:

\[\mathrm{Transmitter}\;\mathrm{site:}\;\;\]
\[\mathrm{Receiver}\;\mathrm{site}:\;\;\]
\[\mathrm{sum}=\frac{\mathrm L+\mathrm R}2\;\;\]
\[\mathrm L=\mathrm{sum}+\mathrm{difference}\;\]

\[\mathrm{difference}=\frac{\mathrm L-\mathrm R}2\;\;\]
\[\mathrm R=\mathrm{sum}-\mathrm{difference}\]

With mono reception the difference signal is not evaluated. We can set „difference“ to zero in the dematrixing rules of the receiver site. This means L=R=sum. The L and R channels have the same signal and the stereo separation is completely lost.

Considerations about noise and interference

Due to the FM stereo transmission method, the difference signal is much more susceptible to interference than the sum signal (for details see here). Therefore the quality of the audio signal is much better with mono reception. If you have the possibility to switch your home receiver to mono manually, you will notice this.

Your car radio or smartphone automatically reduces the difference signal level when reception becomes poor. A reduced difference signal means less noise at the expense of less stereo effect.

With the patented method, the noise can be reduced without deteriorating the stereo separation. So you will get stereo performance with much less noise even in bad reception conditions, like in the mono case (for this, existing functions of the stereo receiver such as stereo-blend and hi-blend should be switched off).

If you use earphones or headphones, you will notice the improvement in stereo performance and signal-to-noise ratio even more than if you use loudspeakers.

Deriving the rules for the noise-reduction method

Let’s take a look at a the matrixing/dematrixing rules for a single signal, e.g. a speech signal recorded with one microphone and split into the right and left audio channel.

If we assume that on the transmitting end there is no excess width of the stereo base (in other words R=0 and L=0 represent the extreme locations of the stereo base), then the matrixing rules yield:

\[\mathrm{for}\;\mathrm R=0\;:\]
\[\mathrm{and}\;\mathrm{for}\;\mathrm L=0\;:\]
\[\mathrm{deriving}\;:\]
\[\mathrm{difference}=\mathrm{sum}\]
\[\mathrm{difference}=-\mathrm{sum}\]
\[\left|\mathrm{difference}\right|=\left|\mathrm{sum}\right|\]

Regarding the single signal, for each spot mapped within the stereo base, the rule follows:

\[\left|\mathrm{difference}(\mathrm t)\right|\leq\left|\mathrm{sum}(\mathrm t)\right|\]

where the equality holds true for the cases R=0 and L=0.

With the same consideration, the following rule can be defined for the magnitude spectra in the frequency domain **:

\[\left|\mathrm{Difference}(\mathrm\omega)\right|\;\leq\;\left|\mathrm{Sum}(\mathrm\omega)\right|\\\\\]

This means that the frequency components (spectral lines) of the difference signal magnitude spectrum are not higher than those of the sum signal magnitude spectrum, otherwise the signal will be outside the stereo base.

Fig. 3 shows an example of a sum signal magnitude spectrum (red) and a difference signal magnitude spectrum (blue). Normally, the blue curve lies below the red curve. However, in this case, noise in some parts of the frequency spectrum has shifted the blue curve above the red curve. These blue parts can be lowered to the red curve without restricting the stereo base. The amount of attenuation is shown in the black curve. All curves are given in logarithmic measure [dB].

Sum and difference signal spectra
Figure 3 | Snapshot of sum and difference signal spectra

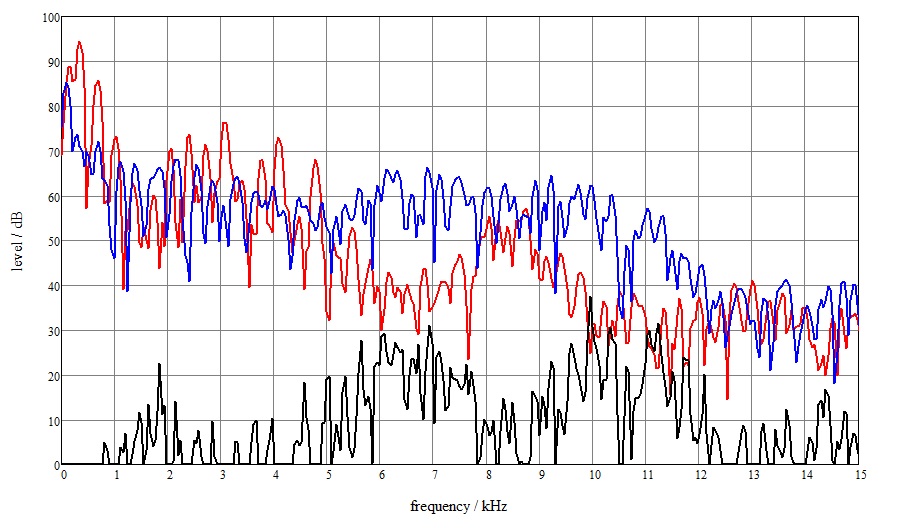
The reduction of the difference signal magnitude spectrum to the sum signal magnitude spectrum at some frequencies means that the noise is attenuated there. In the apparent case of a useful sine signal at e.g. 1000 Hz, all other parts of the difference signal magnitude spectrum would be suppressed.

In other words, noise is reduced by eliminating the excessive width of the stereo base caused by noise.

For a more detailed and comprehensive technical discussion, please download my article in the Journal of the Audio Engineering Society (JAES) here. It also contains information on compatibility with other analog or digital transmission systems and on all types of interference that can be reduced. Some of them are noted here:

  • random FM noise
  • ACI (adjacent channel interference)
  • EMI (electromagnetic interference)
  • multipath interference
  • interference from IBOC signals
  • combined interference

Notes: